Caracterización de los personajes

 

El encuadre

https://educacionplasticayvisual.com/comunicacion-audiovisual/encuadre-y-tipos-de-plano/

Luz y Volumen

 https://epvabelenjminfantes.blogspot.com/2020/05/

perspectiva militar

 

Perspectiva Cónica Oblicua

 

http://www.getloupe.com/v/ke8zepn8

Perspectiva Cónica

 En esta tarea vamos a aplicar los fundamentos de la perspectiva cónica frontal para dibujar una habitación con baldosas cuadradas. 

Para ello colocaremos la LT a 3cm del borde del papel y la LH a 7cm de la LT. El punto Principal P estará en la LH. Como distancia principal pondremos 10cm y situaremos los puntos D y D´ a un lado y otro de P. La línea de tierra la dividiremos en segmentos de 3cm de lado. La altura de la habitación en la línea de tierra será de 15cm y tendrá 7 baldosas de profundidad. 

Una vez dibujada las paredes y suelo embaldosado de la habitación dibujaremos alguna puerta o ventana. luego la decoraremos como queramos, poniendo algún mueble y, por último, le damos color. Para el color debemos pensar en las ventanas y de donde viene la luz para ensombrecer unas paredes más que otras.

Saturación del color.

En esta lámina vamos a dividir el espacio de la hoja en dos partes iguales, dejando un pequeño margen entre ellas, como en el ejemplo. En estos recuadros vamos a hacer un dibujo libre, no tiene por qué ser figurativo, pueden ser formas abstractas, geométricas o no, que segmenten el espacio para luego colorearlo. Los dibujos pueden ser o no similares en cada una de las mitades.

Ahora vamos a colorear cada uno de los recuadros. El primero lo colorearemos con colores saturados, para ello cogemos los primarios y secundarios y vamos dando color a los espacios apretando nuestro lápiz para que no queden espacios en blanco, obteniendo colores muy intensos. El segundo recuadro lo colorearemos con colores mezclados con negro, gris, marrón... o apretando poquito el lápiz , que sería como mezclarlo con el blanco, obteniendo colores tenues y apagados.

Escalas cromáticas

 

Armonías cromáticas

 

Módulos equivalentes

Otra de las transformaciones que podemos aplicar a un módulo es la equivalencia. Recordamos que dos formas distintas son equivalentes si tienen el mismo área. En esta tarea vamos a crear formas equivalentes al cuadrado que se convertirán en el módulo con el que crearemos nuestra red modular. Como se ha hecho en los archivos adjuntos, a partir de un cuadrado (construido con cuadraditos de la hoja de tu cuaderno) realizaremos modificaciones para crear otra forma irregular, pero equivalente al cuadrado. Esta forma será el módulo que luego repetiremos, al menos 9 veces, para construir la red modular. Puedes reducir la escala del módulo para crear la red , de manera que quepa correctamente en la hoja de tu cuaderno. Para que la tarea esté completa deberá haber, al menos, tres ejemplos.

Lotte Reiniger

El primer largometraje de cine animado que se conserva es de la cineasta Lotte Reiniger

En ella se encuentran los orígenes del mundo del cine animado. Dedicó tres años de su vida a crear el largometraje animado Las aventuras del príncipe Achmed, el primer largometraje de animación que se conserva.

Una película de siluetas es una solución intermedia entre el teatro de sombras y lo que conocemos como dibujos animados, sin ser ninguna de las dos cosas. Reiniger colocaba sus recortes articulados sobre una pantalla iluminada (con distintos fondos para ambientar en cada caso) y los filmaba fotograma a fotograma añadiendo pequeños cambios. 24 imágenes por segundo. Resultado: siluetas negras que discurren con ilusión de movimiento, es decir, la técnica del «stop motion» aplicada, no a objetos tridimensionales, sino a formas cerradas (siluetas) que dejan al espectador imaginarlo prácticamente todo. Según Lotte Reiniger, «Una película de siluetas es una película de figuras negras de contornos claramente definidos, una película de recortes a tijera. De inspiración en el teatro de sombras chinescas, las películas de siluetas tienen una técnica muy precisa, sólo son necesarias unas tijeras, cartón negro, papel de calcar, hilo o alambre, algo de plomo, una cámara, bombillas, una placa de vidrio, madera para construir una mesa de fotografía y… mucha paciencia».

Reiniger se anticipó en una década tanto a Walt Disney como a Ub Iwerks en utilizar la cámara multiplano para crear efecto de tridimensionalidad.

https://www.youtube.com/watch?v=EagTdA1RN1Q

Ilustración en contra de la Violencia de Género

 

Malota

Estelí Meza

Pum Pum

Redes Modulares

Una red modular es una estructura en la que se relacionan figuras iguales o semejantes. Esta estructura, generalmente geométrica, es como una malla de formas cuadrangulares, triangulares o derivadas que cubren toda la superficie. 

Módulo

Modulo es la unidad, la figura que se va a repetir formando la malla o red. 

Tipos de redes modulares

. Simples: formadas por la repetición de una misma figura. 

. Compuestas: formadas por la repetición de varias figuras o la superposición de varias redes simples. 

Supermódulo:

A un módulo se le pueden aplicar unos movimientos o transformaciones para dar movimiento y ritmo a la red, con la combinación de varios módulos y una transformación obtenemos un supermódulo. 

Los movimientos y transformaciones que podemos aplicar al módulo son la traslación, la simetría, el giro y la equivalencia. 

También se pueden combinar colores y el positivo - negativo de una misma figura para hacer más dinámica la composición modular o red. 

Composiciones modulares basadas en la circunferencia.

No existen redes modulares basadas en la circunferencia ya que las circunferencias no pueden compactarse por ser curvas, quedando espacios entre ellas. No obstante, si se pueden emplear inscribiéndolas en otras estructuras poligonales. Estos módulos pueden dar lugar a distintas relaciones entre las formas circulares: distanciamiento, toque, unión, sustracción o intersección.

Tridimensionalidad.

Con las composiciones modulares se puede crear sensación de tridimensionalidad. 

En una hoja cuadriculada de tu cuaderno vas a inventar, al menos, cuatro módulos distintos. Para ello dibujaremos cuadrados de 4x4 cuadraditos de tu cuaderno, en ese cuadrado dibujarás un módulo no simétrico. Siguiendo el mismo proceso diseñarás otros modelos. Luego dibujaremos los negativos de cada diseño, invirtiendo los tonos. Escogerás uno de tus diseños para hacer combinaciones de cuatro, lo que llamamos supermódulo. Las combinaciones las haremos basándonos en los movimientos y transformaciones ya aprendidas en una tarea anterior: traslación, simetría, giro... Procura hacer tantos supermódulos como puedas. Por ultimo, dibujaremos la red modular. Escogeremos uno de los supermódulos y lo repetiremos, al menos, 4 veces (16 módulos). En el ejemplo se han dibujado dos redes modulares. La primera a escala natural 1:1 y la segunda a escala de ampliación 3:2 .

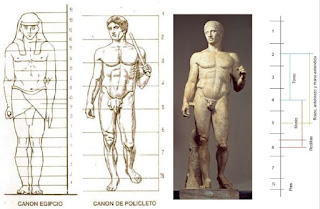
Proporciones del cuerpo humano

 Proporción es la relación comparativa de una cosa con respecto a otra o de una parte con el todo. En esta tarea vanos a estudiar la proporción del cuerpo humano, comparando una parte (cabeza, puño...) con la totalidad. De la observación de la realidad se establece una norma para representar el cuerpo humano, estableciendo una proporción entre una parte(cabeza, puño...) con el resto. A esta norma se le llama CANON.

Así, los egipcios establecieron el canon de 18 puños, los griegos el de 7 cabezas y media y Leonardo da Vinci, en el Renacimiento, el canon de 8 cabezas.

En una hoja cuadriculada de tu cuaderno vamos a representar una figura humana siguiendo el canon egipcio. Realizaremos una cuadricula de 19 cuadrados de alto por 10 de ancho. Para que tu dibujo no quede a una escala muy pequeña, cada cuadrado estará formado por 4 cuadritos. En vuestra cuadrícula copiaréis la figura que aparece aquí. Tenéis que fijaros muy bien en que cuadrito se sitúa cada elemento. Es mejor que empecéis situando algunas partes concretas como los hombros, la nariz, manos, pies, cintura...

Cuando acabéis de copiar la figura podéis caracterizarla, según una época concreta o un estilo de vuestro gusto.

En algunos dibujos, pinturas y esculturas vemos que las proporciones son antinaturales, no guarden la regla o canon que hemos visto anteriormente. Son deformaciones que se hacen con carácter estético o expresivo y dependen del valor simbólico que se le quiere dar al objeto representado.

Dibujaremos, ahora, una cuadricula de 8 cuadrados de alto x 8 de ancho, cada cuadrado debe estar formado por cuatro cuadritos. En ella vamos a copiar una figura cuyas proporciones tienen un carácter expresivo, "Supernena". Siguiendo el mismo procedimiento que antes, nos fijaremos en que cuadrito se sitúa cada elemento. En el dibujo de "Supernena", ¿Qué relación o proporción hay entre la cabeza y el resto de la figura?

Proporción y escalas

Primero, vamos a realizar una pajarita de papel dividiendo un A4 por la mitad. Después, la esconderemos e intentaremos dibujarla de memoria. No os preocupéis del resultado, es para demostraros lo importantes que son las proporciones en un dibujo. Una pajarita de papel está inscrita en un cuadrado y sus partes son subdivisiones del cuadrado, trazando las diagonales y dividiendo el cuadrado en otros más pequeños.

La pajarita de papel, que hemos realizado, tiene unas dimensiones concretas y va a ser nuestro referente en esta tarea. Cogiendo una hoja de cuadros, la vamos a dibujar con sus dimensiones reales (estará inscrita en un cuadrado de 18x18 si los cuadrados de nuestra hoja son pequeños, o de 15x15 si nuestra hoja es de cuadrados grandes) La escala de este primer dibujo es la escala natural, 1:1. Realizaremos otros dibujos aplicando una escala de reducción, pueden ser de escala 1:2 o 2:3. Por último, haremos un dibujo aplicando una escala de ampliación, por ejemplo la escala 3:2.

Esto mismo de las escalas, que hemos hecho con el dibujo de la pajarita, lo vamos a repetir con otra figura sencilla. La dibujaremos con unas medidas que consideraremos como escala natural y la repetiremos ampliándola y reduciéndola. En cada dibujo indicaremos la escala. En los archivos adjuntos tenéis varios modelos de dibujos sencillos, algunos son de papiroflexia y otros son diseños sobre una hoja cuadriculada. Podéis escoger algunos de estos modelos o inventaros el vuestro.